原码,反码,补码
由计算机的硬件决定,任何存储于计算机中的数据,其本质都是以二进制码存储。根据冯~诺依曼提出的经典计算机体系结构框架。一台计算机由运算器,控制器,存储器,输入和输出设备组成。其中运算器,只有加法运算器,没有减法运算器(据说一开始是有的,后来由于减法器硬件开销太大,被废了 )所以,计算机中的没法直接做减法的,它的减法是通过加法来实现的。你也许会说,现实世界中所有的减法也可以当成加法的,减去一个数,可以看作加上这个数的相反数。当然没错,但是前提是要先有负数的概念。这就为什么不得不引入一个该死的符号位。
而且从硬件的角度上看,只有正数加负数才算减法。正数与正数相加,负数与负数相加,其实都可以通过加法器直接相加。
原码,反码,补码的产生过程,就是为了解决,计算机做减法和引入符号位(正号和负号)的问题。
在原码,反码表示法中,我们把减法化为加法的思维是减去一个数,等于加上一个数的相反数,结果发现引入了符号位,却因为符号位造成了各种意向不到的问题。但是从上面的例子中,我们可以看到其实减去一个数,
对于数值有限制,有溢出的运算(模运算)来说,其实也相当于加上这个数的同余数。也就是说,我们
不引入负数的概念,就可以把减法当成加法来算。所以接下来我们聊4位二进制数的运算,也不必急于引入符号位。因为补码的思想,把减法当成加法时并不是必须要引入符号位的。而且我们可以通过下面的例子,也许能回答另一个问题,
为什么负数的符号位是‘1’,而不是正数的符号位是‘1’。
原码:是最简单的机器数表示法。用最高位表示符号位,‘1’表示负号,‘0’表示正号。其他位存放该数的二进制的绝对值。
若以带符号位的四位二进值数为例
1010 : 最高位为‘1’,表示这是一个负数,其他三位为‘010’,即(0*2^2)+(1*2^1)+(0*2^0)=2(‘^’表示幂运算符)所以1010表示十进制数(-2)。
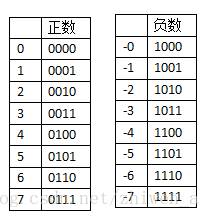
下图给出部份正负数数的二进制原码表示法
OK,原码表示法很简单有没有,虽然出现了+0和-0,但是直观易懂。
于是,我们高兴的开始运算。
0001+0010=0011 (1+2=3)OK0000+1000=1000 (+0+(-0)=-0) 额,问题不大0001+1001=1010 (1+(-1)=-2)
噢,1+(-1)=-2,这仿佛是在逗我呢。
于是我们可以看到其实正数之间的加法通常是不会出错的,因为它就是一个很简单的二进制加法。
而正数与负数相加,或负数与负数相加,就要引起莫名其妙的结果,这都是该死的符号位引起的。0分为+0和-0也是因他而起。
所以原码,虽然直观易懂,易于正值转换。但用来实现加减法的话,运算规则总归是太复杂。于是反码来了。
反码:
正数的反码还是等于原码
负数的反码就是他的原码除符号位外,按位取反。
若以带符号位的四位二进制数为例:
3是正数,反码与原码相同,则可以表示为0011-3的原码是1011,符号位保持不变,低三位(011)按位取反得(100)所以-3的反码为1100
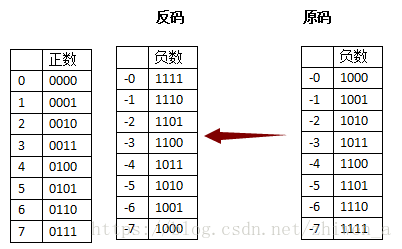
下图给出部分正负数的二进制数反码表示法
对着上图,我们再试着用反码的方式解决一下原码的问题
0001+1110=1111 (1+(-1)= - 0)
互为相反数相加等于0,解决。
虽然是得到的结果是1111也就是-0(补码解决该问题)
好,我们再试着做一下两个负数相加
1110(-1)+1101(-2)=1011(-4) 1011结果为反码 (-4为原码)
噢,好像又出现了新问题
(-1)+(-2)=(-4)?
不过好像问题不大,因为1011(是-4的反码,但是从原码来看,他其实是-3。巧合吗?)
我们再看个例子吧
1110(-1)+1100(-3)=1010(-5)
确实是巧合,看来相反数问题是解决了,但是却让两个负数相加的出错了。
但是实际上,两个负数相加出错其实问题不大。我们回头想想我们的目的是什么?是解决做减法的问题,把减法当成加法来算。
两个正数相加和两个负数相加,其实都是一个加法问题,只是有无符号位罢了。而正数+负数才是真正的减法问题。
也就是说只要正数+负数不会出错,那么就没问题了。负数加负数出错没关系的,负数的本质就是正数加上一个符号位而已。
在原码表示法中两个负数相加,其实在不溢出的情况下结果就只有符号位出错而已(1001+1010=0011)
反码的负数相加出错,其实问题不大。我们只需要加实现两个负数加法时,将两个负数反码包括符号位全部按位取反相加,然后再给他的符号位强行置‘1’就可以了。
所以反码表示法其实已经解决了减法的问题,他不仅不会像原码那样出现两个相反数相加不为零的情况,而且对于任意的一个正数加负数,如:0001(1)+1101(-2)=1110(-1) 计算结果是正确的。所以反码与原码比较,最大的优点,就在于解决了减法的问题。
但是我们还是不满足为什么 0001+1110=1111 (1+(-1)=-0) 为什么是-0呢
而且虽然说两个负数相加问题不大,但是问题不大,也是问题呀。好吧,处女座。接下来就介绍我们的大boss补码。
补码:
- 正数的补码等于他的原码
- 负数的补码等于反码+1。(这只是一种算补码的方式,多数书对于补码就是这句话)
在《计算机组成原理中》,补码的另外一种算法 是
负数的补码等于他的原码自低位向高位,尾数的第一个‘1’及其右边的‘0’保持不变,左边的各位按位取反,符号位不变。
总结:
- 负数的补码等于反码加一
- 反码是原码除符号位,按位取反。补码等于反码加一
Java中的<< 和 >> 和 >>> 详细分析
<<表示左移移,不分正负数,低位补0;
注:以下数据类型默认为byte-8位
左移时不管正负,低位补0
正数:r = 20 << 2
20的二进制补码:0001 0100
向左移动两位后:0101 0000
结果:r = 80
负数:r = -20 << 2
-20 的二进制原码 :1001 0100
-20 的二进制反码 :1110 1011
-20 的二进制补码 :1110 1100
左移两位后的补码:1011 0000
反码: 1010 1111
原码:1101 0000
结果:*r = -80
*
>>表示右移,如果该数为正,则高位补0,若为负数,则高位补1;
注:以下数据类型默认为byte-8位
正数:r = 20 >> 2
20的二进制补码:0001 0100
向右移动两位后:0000 0101
结果:r = 5
负数:r = -20 >> 2
-20 的二进制原码 :1001 0100
-20 的二进制反码 *:1110 1011
*
-20 的二进制补码 :1110 1100
右移两位后的补码:1111 1011
反码:1111 1010
原码:1000 0101
结果:r = -5
>>>表示无符号右移,也叫逻辑右移,即若该数为正,则高位补0,而若该数为负数,则右移后高位同样补0
正数: r = 20 >>> 2
的结果与 r = 20 >> 2 相同;
负数: r = -20 >>> 2
注:以下数据类型默认为int 32位
-20:源码:10000000 00000000 00000000 00010100
反码:11111111 11111111 11111111 11101011
补码:11111111 11111111 11111111 11101100
右移:00111111 11111111 11111111 11111011
结果:r = 1073741819